Digitale Signalverarbeitung

Seit Jahrzehnten hält die Digitaltechnik die Klangverarbeitung fest in ihrem Griff. Spätestens seit den 1990er Jahren wird alles, was Audiosignale verarbeitet, digitalisiert. Mitte der 90er waren erstmals voll-digitale Tonstudios kein bloßer Traum mehr, beispielsweise durch die Einführung des Yamaha 02R-Mischpults für gut 10.000$. Aber auch der kleine Geldbeutel wurde bedient, etwa mit digitalen Effektgeräten, die die klappernden Hallspiralen oder tonnenschweren Hallplatten überflüssig machten. Doch was bedeutet es, wenn ein Klang digital verarbeitet wird? Dies soll hier in aller Kürze angerissen werden. Dabei stellt sich zunächst die Frage, was „analog“ bzw. „digital“ in der Audiotechnik bedeuten soll.

analog

Wir leben in einer analogen Welt. Auch die Physik, die uns umgibt und bestimmt, ist rein analog (die Quantenmechanik lassen wir außen vor). Dabei ist analog nicht ganz das richtige Wort, jedenfalls nicht in seiner ursprünglichen Bedeutung (von griechisch ἀνάλογος/análogos: „entsprechend, verhältnismäßig, sinngemäß“). Besser ist: kontinuierlich. Alles um uns herum geschieht kontinuierlich. So z.B. auch der Schall. Das Fell einer geschlagenen Trommel schwingt kontinuierlich, d.h. es ändert in jedem Moment seine Position, verdrängt dabei kontinuierlich die Luftmoleküle und bringt sie letztendlich zum Schwingen. Ein analoges, kontinuierliches akustisches Signal entsteht. Dieses kann von einem Mikrofon empfangen und in elektrische Spannung umgewandelt werden. Und hier passt die ursprüngliche Wortbedeutung von „analog“ nun doch wieder, denn dieses Spannungssignal folgt der Luftschwingung, die es repräsentiert – die Spannug verläuft analog zum Schalldruck (wenn es gut läuft).

Die Ausgangsspannung dieses Mikrofons können wir einem Audiogerät zuführen, z.B. einem Mischpultkanal. Dieser wird das kontinuierlich schwankende Spannungssignal weiterverarbeiten. Analoge Geräte tun das mithilfe zahlloser elektronischer Verstärker, die auf dem gesamten Signalweg zwischen Geräte-Eingang und Geräte-Ausgang ihr Werk verrichten. Das Wort „Verstärker“ ist hierbei ein rein elektrotechnischer Begriff. Auch, wenn ein Signal abgeschwächt oder gefiltert wird, sind letztlich winzige (Transistor-)Verstärker im Spiel – entsprechend beschaltet und eingestellt. Und jeder davon arbeitet eben kontinuierlich: Ein Signal am Eingang beeinflusst direkt viele einzelne Spannungen und Ströme innerhalb des Verstärkers entsprechend des Signalpegels. Und dieses Signal erscheint genau so (oder verstärkt, abgeschwächt oder gefiltert) wieder am Ausgang des Verstärkers. Das klingt simpel, war aber vor vielen Jahrzehnten absolute Hi-Tech (die Elektronenröhre wurde um 1900 entwickelt, der Transistor etwa 50 Jahre später), und ist auch heute keine triviale Angelegenheit.

Analoges Audiogerät: Eine Reihe von analogen Verstärkern übernimmt die Aufgaben der Signalverarbeitung

digital

Digitale Geräte arbeiten grundsätzlich anders. Sie sind Computer (meist sehr speziell optimiert), also digitale Rechenmaschinen. Ein analog vorliegendes Eingangssignal wird sehr früh im Signalweg digitalisiert (analog/digital-Wandlung; A/D-Wandlung). Das bedeutet, dass es entsprechend seines zeitlichen Verlaufs in viele aufeinanderfolgende Zahlenwerte übertragen wird (engl. digit: „Ziffer, Zahl“). Diese werden anschließend verrechnet, manipuliert und weitergereicht. Erst sehr weit hinten in der Signalkette werden sie wieder in analoge elektronische Signale umgewandelt (D/A-Wandlung; z.B. zur Ansteuerung eines Lausprechers).

Digitales Audiogerät: Das analoge Signal wird digitalisiert (ADC), im Rechner verarbeitet und dann wieder in ein analoges Signal zurückgewandelt (DAC)

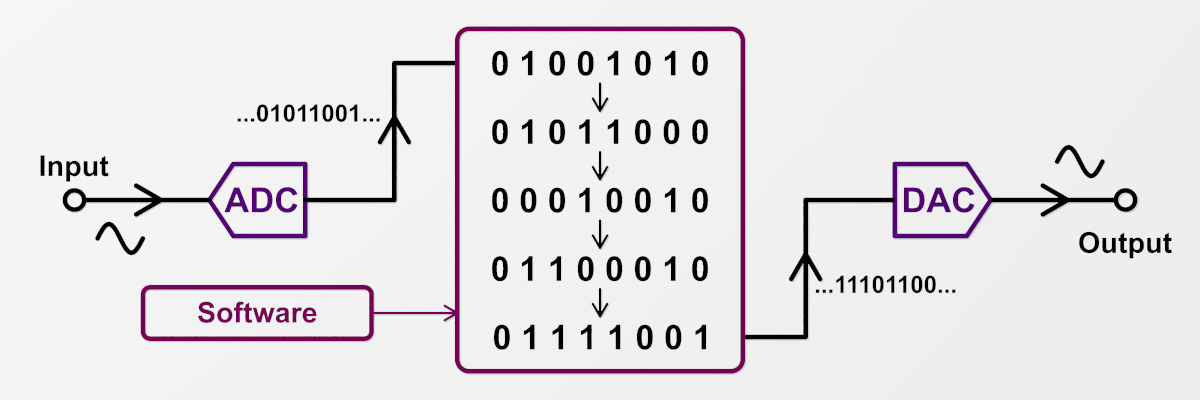
Das Grundprinzip der digitalen Audiotechnik ist also das „Zerhacken“ eines analogen Signals in aufeinanderfolgende Zahlen. Dies geschieht nicht kontinuierlich, sondern zeitdiskret, d.h. zu ganz bestimmten, regelmäßigen Zeitpunkten. In einem A/D-Wandler (ADC; A/D-Converter) wird das Signal „abgetastet“, also immer wieder neu vermessen, und anschließend durch aufeinanderfolgende Zahlenwerte repräsentiert. Im D/A-Wandler (DAC; D/A-Converter) geschieht das Gegenteil: die stetige Reihe von Zahlen wird wieder in eine elektrische Spannung umgesetzt, die wieder kontinuierlich ihren Wert verändert.

Das Digitalisieren eines analogen Signals wird auch Sampling genannt (engl. to sample: „probieren, abfragen“). Ein einzelner Zahlenwert aus der Zahlenreihe ist ein Sample. Wir haben gelernt, dass das Signal, das diese Samples repräsentieren, nicht mehr kontinuierlich, sondern zeitdiskret ist. Zusätzlich ist es aber auch quantisiert, d.h. beschränkt auf bestimmte Wertestufen. Der Wertebereich der Zahlen, die der A/D-Wamdler ausspuckt, ist nämlich beschränkt; beispielsweise auf ganze Zahlen. Zahlen mit Nachkommastellen sind dann nicht möglich, und so muss bei jeder Abtastung gerundet werden. Dies ist eindeutig eine Verfälschung des Signals. Während ein analoges Signal kontinuierlich jeden Wert annehmen kann, besteht ein digitales nur aus Stichproben, die noch dazu gerundet sind.

Digitalisierung durch Abtastung: Zu diskreten Zeitpunkten wird das Signal vermessen; das Ergebnis sind Zahlen, die gerundet (quantisiert) werden müssen

Kaum vorstellbar, dass ein auf diese Weise misshandeltes Audiosignal noch gut klingen kann. Damit dies wider Erwarten doch der Fall ist, sind zwei Kenngrößen entscheidend: Die Abtastrate und die Auflösung.

Abtastrate / Samplingfrequenz

Damit das digitale Signal den schnellen Änderungen einer akustischen Schwingung folgen kann, müssen die einzelnen Samples zeitlich möglichst schnell aufeinander folgen. Tatsächlich dürfen zwei Samples kaum länger als 25µs (0.000025 Sekunden) auseinanderliegen, um eine gute Klangqualität zu erreichen. Dies ist eine unvorstellbar kurze Zeit und entspricht 40.000 Samples pro Sekunde oder einer Abtastfrequenz (Abtastrate, Samplingfrequenz) von 40kHz. In der Praxis haben sich eine Reihe von Standard-Abtastraten etabliert: 44,1kHz (Audio-CD), 48kHz, 96kHz oder 192kHz. Bei 192kHz sind es schon nur noch etwa 5µs Abtastintervall.

Warum ist gerade 40kHz das Minimum für gute Klangqualität? Dies folgt direkt aus dem (Nyquist-Shannon-)Abtasttheorem. Es besagt: Ein Signal, das Frequenzen bis zu einer maximalen Frequenz f_max enthält, muss mit einer Samplingfrequenz von mindestens 2⋅f_max abgetastet werden, damit es ohne Informationsverlust durch die entstehende Zahlenfolge repräsentiert wird. Hinter dieser Erkentnis steckt so viel Mathematik (s. z.B. bei Wikipedia), dass ich das an dieser Stelle nicht weiter vertiefe und einfach mal so hinnehme :-) Da das vom Menschen hörbare Audiospektrum bis etwa 20.000Hz hinaufreicht, ergeben sich als minimale Samplingfrequenz die 40.000Hz. Beschränkt man das Audiosignal künstlich, kommt man mit kleineren Abtastraten aus. In der digitalen Telefontechnik ISDN beispielsweise wird (wurde) mit 8kHz digitalisiert. Die Bandbreite reicht hier bis ca 3,4kHz hinauf, was für reine Sprachverständlichkeit (leidlich) ausreicht.

Auflösung / Wortbreite / Bittiefe

Samplewerte sind Zahlen. In der Computertechnik ist jede Zahl eine Binärzahl. Sie besteht aus Bits (0 oder 1) und ist auf eine bestimmte Stellenanzahl begrenzt (z.B. 16Bit). Dadurch ist der mögliche Wertebereich begrenzt (Auflösung). Ein Sampleergebnis, das eigentlich zwischen zwei benachbarten Werten liegt, muss also gerundet werden, um ins Schema zu passen. Diese Quantisierung bedeutet ein Verfälschen des Signals, da die Information über den genauen Signal-Wert unwiederbringlich verloren geht. Ist die zur Verfügung stehende Auflösung zu klein, dann äußert sich dies in hörbarem Signalrauschen (Quantisierungsrauschen).

Ziel muss es also sein, einen ausreichend großen Wertevorrat vorzusehen. In der digitalen Audiotechnik sind es üblicherweise 16Bit (Audio-CD), 24 oder 32Bit. Damit sind zwischen vielen Tausend und einigen Milliarden Wertezuständen möglich. In der o.g. Telefontechnik ISDN sind es nur 8Bit (256 Zustände), was sich neben der niedrigen Abtastrate deutlich in der Tonqualität niederschlägt.

Qualität

Ein „Klang“ in einem digitalen Audiogerät ist also ein zerhacktes Signal aus Zahlen-Treppchen. Jeder von uns kennt Beispiele, bei denen so etwas gar nicht gut klingt: Musik oder Sprache aus elektronischen Kinderspielzeugen beispielsweise, oder das Gedudel aus elektronischen Grußkarten. Beides ist oft eine Beleidigung für die Ohren und klingt schräbbelig und anstrengend. Doch schon bei der Audio-CD, die um 1980 herum entwickelt wurde, ist das völlig anders. Mit einer Abtastrate von 44,1kHz und einer Wortbreite von nur 16Bit scheint sie aus heutiger Sicht mit der heißen Nadel gestrickt zu sein – und doch klingt Musik von einer solchen Silberscheibe exzellent. Warum werden dann heutzutage noch höhere Werte angesetzt?

Nun, ein CD-Player gibt einfach nur gespeicherte Musik wieder. Der Klang wird nicht groß verarbeitet, sondern „nur“ an die (analogen) Ausgangsbuchsen weitergegeben. In einem digitalen Mischpult oder Tonstudio ist das anders. Hier geschehen in jedem einzelnen Kanal unzählige Rechenoperationen: Pegel, Kompressor, Klangregelung, ... all dies ist reine Mathematik. Und bei jeder einzelnen binären Rechnung entstehen wieder Rundungsdifferenzen – die sich dann summieren. Aus diesem Grund und vielen weiteren, die in der Theorie der digitalen Signalverarbeitung zu suchen sind (z.B. Spiegelfrequenzen), arbeiten professionelle Geräte mit großzügigeren Parametern: Üblich sind inzwischen 96 oder gar 192kHz bei 24-64 Bit. Rundungsdifferenzen und hörbare Artefakte werden dadurch in kleineren Rahmen gehalten, sodass sie auch nach zigtausend Berechnungen nicht hörbar sind. Klar, dass dies auf der anderen Seite die Rechenleistung massiv erhöht. Der Verbesserung der Klangqualität sind also durchaus Grenzen gesetzt.

Signalverarbeitung

Doch wie geschieht nun die Signalverarbeitung in einem digitalen Audio-Gerät? Nun, dies hier zu beantworten, würde den Rahmen dieser gesamten Website sprengen. Ganze Studienbereiche beschäftigen sich mit der arithmetischen Signalverarbeitung. Fourier-Analyse, Faltungsoperatoren, Imulsantwort, rekursive und nichtrekursive Filter – es steckt eine Menge höhere Mathematik darin und bleibt wohl für immer den Mathe-Assen vorbehalten. Doch so viel ist auch für den Laien verständlich: Habe ich ein Signal in Form einer Zahlenfolge und multipliziere ich jede einzelne Zahl mit dem Faktor 2, dann habe ich am Ende dasselbe Signal, nur um den Faktor 2 verstärkt (also lauter). Multipliziere ich mit 0,5, dann wird es leiser. Multipliziere ich mit 0, dann verschwindet es ganz. Und genau dies geschieht mit dem Signal eines digitalen Mischpultkanals, wenn ich den Fader ganz auf Null ziehe (bzw. -∞dB).

Noch ein weiteres Beispiel ist leicht verständlich: der Echo-Effekt (Delay). In analogen Zeiten war es schwer, ein Echo zu erzeugen. Verwendet wurden Bandmaschinen, in denen ein Tonkopf das Signal auf Band aufnahm. In direkter Nähe zu diesem Tonkopf befand sich ein weiterer Tonkopf, der die wenige Millisekunden alte Aufnahme dann wieder abspielte: als Echo. Die Echo-Zeit wurde dabei bestimmt durch den Tonkopfabstand und die Bandgeschwindigkeit. Für längere Delays wurden sogar zwei Bandmaschinen miteinander gekoppelt. In digitalen Zeiten ist das Echo wohl eines der leichtesten Übungen (wenn genügend Speicher zur Verfügung steht). Das Signal vom Eingang wird einfach zwischengespeichert. Nach einer gewissen Anzahl von Samples (Echo-Zeit geteilt durch Sample-Zeit) wird das gespeicherte Signal dann wieder ausgelesen und dem Ausgang zugeführt. Fertig ist das Echo.

Analoges in der Digitaltechnik

Genau wie eine analoge Schaltung muss auch ein digitales Rechenwerk ordentlich ausgesteuert sein.

• Ist der Signalpegel zu niedrig, dann entstehen in analogen Systemen hörbare Nebengeräusche, hervorgerufen durch thermisches Rauschen der Bauteile oder Brummeinstreuung von außen. In der digitalen Welt dagegen sind es die Rundungsdifferenzen, die hörbar werden, wenn nur ein kleiner Teil der zur Verfügung stehenden Auflösung genutzt wird. Es entsteht Quantisierungsrauschen. (Selbstverständlich werden die Rundungsdifferenzen nicht per se durch die geringe Aussteuerung hörbar. Erst, wenn das Nutzsignal anschließend in ungewöhnlichem Maße verstärkt werden muss, damit überhaupt etwas aus den Lautsprechern kommt, werden mit ihm gemeinsam auch die Störgeräuschen verstärkt.)
• Ist der Signalpegel zu hoch, können analoge Verstärkerschaltungen leicht übersteuert werden und erzeugen Signal-Verzerrungen durch nichtlineares Verhalten. In einer digitalen Signalkette dagegen erschöpft sich bei zu hohem Pegel schlicht der Wertevorrat der arithmetischen Berechnungen. Eine höhere Zahl als die maximal mögliche kann nun einmal nicht gespeichert und verarbeitet werden. In beiden Fällen wird das Signal an seinen Spitzen mehr oder weniger hart abgeschnitten (Clipping).

Vorverstärker / Gain

Analogen wie digitalen Signalketten ist daher immer ein Eingangsverstärker vorgeschaltet, der den Signalpegel an die speziellen Vorgaben der Hardware anpasst. Bei einem Mischpult, das mit vielen verschiedenen Eingangspegeln fertig werden muss (Mikrofonsignal vs. Line-Pegel), ist dieser Vorverstärker regelbar. Es ist der Gain-Regler, der stets ganz oben bzw. vorne im Mischpultkanal zu finden ist. Interessant ist hierbei, dass dieser Eingangsverstärker auch bei digitalen Pulten immer rein analog ausgeführt ist (wenn auch digital steuerbar). Er ist noch vor dem A/D-Wandler eingefügt und sorgt dafür, dass dieser optimal ausgesteuert wird.

Manche Digi-Pulte haben noch einen weiteren Regler für die Eingangsverstärkung. Er ist meist als „Trim“ bezeichnet und arbeitet nach dem A/D-Wandler, ist also eine reine Rechenvorschrift. Liefert der A/D-Wandler durch schlechte Austeuerung (Gain-Regler) ein verrauschtes oder gecliptes Signal, kann der Trim-Regler das nicht wieder rausreißen. Bei korrektem Gain dient der Trim lediglich zur intenen Pegelanpassung verschiedener Kanäle untereinander.

Tiefpassfilter / Hi-Cut / Lo-Pass

Gain und Hi-Cut vor der A/D-Wandlung: Der regelbare Vorverstärker dient der Pegelanpassung an den A/D-Wandler; das Hi-Cut-Filter (Lo-Pass) entfernt zu hohe Frequenzen vor der A/D-Wandlung (wg. Abtasttheorem)

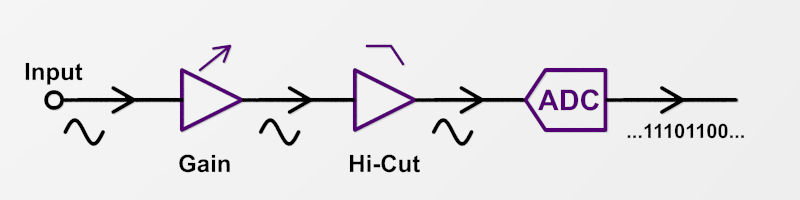
Ein weiteres analoges Element in einem digitalen Audiokanal ist der Tiefpassfilter vor dem A/D-Wandler. Wie oben beschrieben wird beim Abtasttheorem gefordert, dass keine Frequenzen im Analogsignal größer als die halbe Samplingfrequenz auftreten. Wird diese Regel verletzt, wird das gesamte Signal verfälscht in die digitale Welt übertragen. Um dem zu begegnen, wird mit einem steilflankigen Tiefpassfilter das Eingangssignal scharf in der Bandbreite beschnitten: alles eh Unhörbare über ca 20kHz wird abgeschnitten.

Natürlich gibt es keine idealen Filter, die oberhalb einer bestimmten Frequenz nichts mehr durchlassen. Jedes Filter hat eine begrenzte Flankensteilheit. Das bedeutet, dass geringfügig zu hohe Frequenzen zwar bedämpft, aber nicht vollständig eliminiert werden. Erst für noch höhere Frequenzen wird die Bedämpfung dann so groß, dass dieser Signalanteil vernachlässigt werden kann. In dieser Gesetzmäßigkeit liegt ein weiterer Grund, warum eine erhöhte Samplingfrequenz (Überabtastung) vorteilhaft sein kann: Auch mit weniger steilen Eingangsfiltern ist man dabei auf der sicheren Seite, was das Abtasttheorem angeht. Es entsteht einfach „mehr Luft“ zwischen der maximal hörbaren Frequenz und der halben Samplingfrequenz. Das Ergebnis ist eine exaktere A/D-Wandlung.

Vorteile durch Überabtastung: Die nach dem Abtasttheorem kritischen Frequenzen oberhalb f_smpl/2 werden bei Überabtastung effektiver gedämpft: Beispiel mit Tiefpass 2. Ordnung (Grenzfrequenz 20kHz) mit -4,9dB Absenkung bei 24kHz (f_smpl=48kHz) bzw. -8,3dB bei 96kHz (f_smpl=192kHz), und das sogar bei weniger steilem Tiefpass mit doppelter Grenzfrequenz (40kHz).